Difference between revisions of "Neural Network"
m (→Neural Network History) |
m |
||
| Line 33: | Line 33: | ||
| − | <b>Neural Networks (NNs)</b>, also referred to as Artificial neural networks (ANNs) or neural nets, are a mathematical system modeled on the human brain that learns skills by finding patterns in data through layers of artificial neurons, outputting predictions or classifications. Neural Networks are computing systems inspired by the biological neural networks that constitute animal brains. Neural networks can be hardware- (neurons are represented by physical components) or software-based (computer models), and can use a variety of topologies and learning algorithms. A Neural Network is based on a collection of connected units or nodes called artificial neurons, which loosely model the neurons in a biological brain. Each connection, like the synapses in a biological brain, can transmit a signal to other neurons. An artificial neuron receives signals then processes them and can signal neurons connected to it. The "signal" at a connection is a real number, and the output of each neuron is computed by some non-linear function of the sum of its inputs. The connections are called edges. Neurons and edges typically have a weight that adjusts as learning proceeds. The weight increases or decreases the strength of the signal at a connection. Neurons may have a threshold such that a signal is sent only if the aggregate signal crosses that threshold. Typically, neurons are aggregated into layers. Different layers may perform different transformations on their inputs. Signals travel from the first layer (the input layer), to the last layer (the output layer), possibly after traversing the layers multiple times. [https://en.wikipedia.org/wiki/Artificial_neural_network Artificial neural network | Wikipedia] | + | <b>Neural Networks (NNs)</b>, also referred to as Artificial neural networks (ANNs) or neural nets, are a mathematical system modeled on the human brain that learns skills by finding patterns in data through layers of artificial neurons, outputting predictions or classifications. Neural Networks are computing systems inspired by the biological neural networks that constitute animal brains. Neural networks can be hardware- (neurons are represented by physical components) or software-based (computer models), and can use a variety of topologies and learning algorithms. A Neural Network is based on a collection of connected units or nodes called artificial neurons, which loosely model the neurons in a biological brain. Each connection, like the synapses in a biological brain, can transmit a signal to other neurons. An artificial neuron receives signals then processes them and can signal neurons connected to it. The "signal" at a connection is a real number, and the output of each neuron is computed by some non-linear function of the sum of its inputs. The connections are called edges. Neurons and edges typically have a [[Activation Functions#Weights|weight]] that adjusts as learning proceeds. The [[Activation Functions#Weights|weight]] increases or decreases the strength of the signal at a connection. Neurons may have a threshold such that a signal is sent only if the aggregate signal crosses that threshold. Typically, neurons are aggregated into layers. Different layers may perform different transformations on their inputs. Signals travel from the first layer (the input layer), to the last layer (the output layer), possibly after traversing the layers multiple times. [https://en.wikipedia.org/wiki/Artificial_neural_network Artificial neural network | Wikipedia] |
<img src="https://www.drchriseducation.com/wp-content/uploads/2021/05/Neural-Networks-for-Babies.jpg" width="200"> | <img src="https://www.drchriseducation.com/wp-content/uploads/2021/05/Neural-Networks-for-Babies.jpg" width="200"> | ||
| Line 58: | Line 58: | ||
| − | “In approximation theory, both shallow and deep networks are known to approximate any continuous functions at an exponential cost,” the researchers wrote. “However, we proved that for certain types of compositional functions, deep networks of the convolutional type (even without weight sharing) can avoid the curse of dimensionality.” | + | “In approximation theory, both shallow and deep networks are known to approximate any continuous functions at an exponential cost,” the researchers wrote. “However, we proved that for certain types of compositional functions, deep networks of the convolutional type (even without [[Activation Functions#Weights|weight sharing]]) can avoid the curse of dimensionality.” |
| − | The team then set out to explain why deep networks, which tend to be over-parameterized, perform well on out-of-sample data. The researchers demonstrated that for classification problems, given a standard deep network, trained with gradient descent algorithms, it is the direction in the parameter space that matters, rather than the norms or the size of the weights. | + | The team then set out to explain why deep networks, which tend to be over-parameterized, perform well on out-of-sample data. The researchers demonstrated that for classification problems, given a standard deep network, trained with gradient descent algorithms, it is the direction in the parameter space that matters, rather than the norms or the size of the [[Activation Functions#Weights|weights]]. |
The implications are that the dynamics of gradient descent on deep networks are equivalent to those with explicit constraints on both the norm and size of the parameters–the gradient descent converges to the max-margin solution. The team discovered a similarity known to linear models in which vector machines converge to the pseudoinverse solution which aims to minimize the number of solutions. | The implications are that the dynamics of gradient descent on deep networks are equivalent to those with explicit constraints on both the norm and size of the parameters–the gradient descent converges to the max-margin solution. The team discovered a similarity known to linear models in which vector machines converge to the pseudoinverse solution which aims to minimize the number of solutions. | ||
| − | In effect, the team posit that the act of training deep networks serves to provide implicit regularization and norm control. The scientists attribute the ability for deep networks to generalize, sans explicit capacity controls of a regularization term or constraint on the norm of the weights, to the mathematical computation that shows the unit vector (computed from the solution of gradient descent) remains the same, whether or not the constraint is enforced during gradient descent. In other words, deep networks select minimum norm solutions, hence the gradient flow of deep networks with an exponential-type loss locally minimizes the expected error. [https://www.psychologytoday.com/us/blog/the-future-brain/202008/new-ai-study-may-explain-why-deep-learning-works A New AI Study May Explain Why Deep Learning Works MIT researchers’ new theory illuminates machine learning’s black box.| Cami Rosso - Psychology Today] ..[https://www.pnas.org/ PNAS (Proceedings of the National Academy of Sciences of the United States of America) | T. Poggio, A. Banburski, and Q. Liao] | + | In effect, the team posit that the act of training deep networks serves to provide implicit regularization and norm control. The scientists attribute the ability for deep networks to generalize, sans explicit capacity controls of a regularization term or constraint on the norm of the [[Activation Functions#Weights|weights]], to the mathematical computation that shows the unit vector (computed from the solution of gradient descent) remains the same, whether or not the constraint is enforced during gradient descent. In other words, deep networks select minimum norm solutions, hence the gradient flow of deep networks with an exponential-type loss locally minimizes the expected error. [https://www.psychologytoday.com/us/blog/the-future-brain/202008/new-ai-study-may-explain-why-deep-learning-works A New AI Study May Explain Why Deep Learning Works MIT researchers’ new theory illuminates machine learning’s black box.| Cami Rosso - Psychology Today] ..[https://www.pnas.org/ PNAS (Proceedings of the National Academy of Sciences of the United States of America) | T. Poggio, A. Banburski, and Q. Liao] |
Revision as of 08:43, 6 August 2023
YouTube ... Quora ...Google search ...Google News ...Bing News
- Artificial Intelligence (AI) ... Machine Learning (ML) ... Deep Learning ... Neural Network ... Reinforcement ... Learning Techniques
- Neural Architecture
- AI Solver ... Algorithms ... Administration ... Model Search ... Discriminative vs. Generative ... Optimizer ... Train, Validate, and Test
- Reservoir Computing (RC) Architecture
- Backpropagation ... FFNN ... Forward-Forward ... Activation Functions ...Softmax ... Loss ... Boosting ... Gradient Descent ... Hyperparameter ... Manifold Hypothesis ... PCA
- Singularity ... Sentience ... AGI ... Curious Reasoning ... Emergence ... Moonshots ... Explainable AI ... Automated Learning
- Large Language Model (LLM) ... Natural Language Processing (NLP) ...Generation ... Classification ... Understanding ... Translation ... Tools & Services
- Neuroscience News - Neural Networks
- A Beginner's Guide to Neural Networks and Deep Learning | Chris Nicholson - A.I. Wiki pathmind
Neural Networks (NNs), also referred to as Artificial neural networks (ANNs) or neural nets, are a mathematical system modeled on the human brain that learns skills by finding patterns in data through layers of artificial neurons, outputting predictions or classifications. Neural Networks are computing systems inspired by the biological neural networks that constitute animal brains. Neural networks can be hardware- (neurons are represented by physical components) or software-based (computer models), and can use a variety of topologies and learning algorithms. A Neural Network is based on a collection of connected units or nodes called artificial neurons, which loosely model the neurons in a biological brain. Each connection, like the synapses in a biological brain, can transmit a signal to other neurons. An artificial neuron receives signals then processes them and can signal neurons connected to it. The "signal" at a connection is a real number, and the output of each neuron is computed by some non-linear function of the sum of its inputs. The connections are called edges. Neurons and edges typically have a weight that adjusts as learning proceeds. The weight increases or decreases the strength of the signal at a connection. Neurons may have a threshold such that a signal is sent only if the aggregate signal crosses that threshold. Typically, neurons are aggregated into layers. Different layers may perform different transformations on their inputs. Signals travel from the first layer (the input layer), to the last layer (the output layer), possibly after traversing the layers multiple times. Artificial neural network | Wikipedia

Contents
Deep Neural Network (DNN)
- Deep Learning
- Deep Learning’s Uncertainty Principle
- Andrew Ng's Deep Learning
- Deep Learning’s Uncertainty Principle | Carlos E. Perez - Intuition Machine ... Deep Learning Patterns, Methodology and Strategy
Researchers' study | The MIT research trio of Tomaso Poggio, Andrzej Banburski, and Quianli Liao - Center for Brains, Minds, and Machines) compared deep and shallow networks in which both used identical sets of procedures such as pooling, convolution, linear combinations, a fixed nonlinear function of one variable, and dot products. Why do deep networks have great approximation powers, and tend to achieve better results than shallow networks given they are both universal approximators?
The scientists observed that with convolutional deep neural networks with hierarchical locality, this exponential cost vanishes and becomes more linear again. Then they demonstrated that dimensionality can be avoided for deep networks of the convolutional type for certain types of compositional functions. The implications are that for problems with hierarchical locality, such as image classification, deep networks are exponentially more powerful than shallow networks. ...
The scientists observed that with convolutional deep neural networks with hierarchical locality, this exponential cost vanishes and becomes more linear again. Then they demonstrated that dimensionality can be avoided for deep networks of the convolutional type for certain types of compositional functions. The implications are that for problems with hierarchical locality, such as image classification, deep networks are exponentially more powerful than shallow networks.
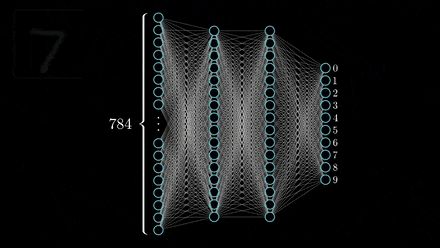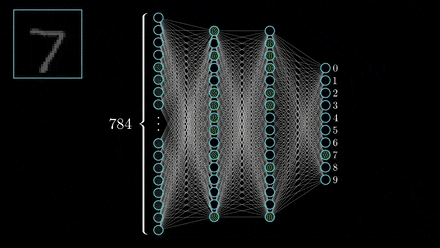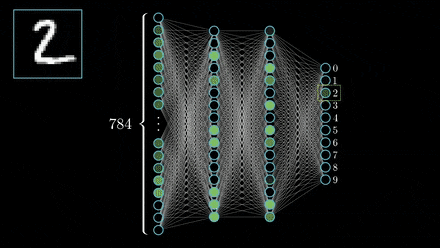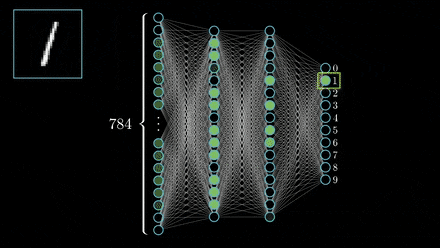
“In approximation theory, both shallow and deep networks are known to approximate any continuous functions at an exponential cost,” the researchers wrote. “However, we proved that for certain types of compositional functions, deep networks of the convolutional type (even without weight sharing) can avoid the curse of dimensionality.”
The team then set out to explain why deep networks, which tend to be over-parameterized, perform well on out-of-sample data. The researchers demonstrated that for classification problems, given a standard deep network, trained with gradient descent algorithms, it is the direction in the parameter space that matters, rather than the norms or the size of the weights.
The implications are that the dynamics of gradient descent on deep networks are equivalent to those with explicit constraints on both the norm and size of the parameters–the gradient descent converges to the max-margin solution. The team discovered a similarity known to linear models in which vector machines converge to the pseudoinverse solution which aims to minimize the number of solutions.
In effect, the team posit that the act of training deep networks serves to provide implicit regularization and norm control. The scientists attribute the ability for deep networks to generalize, sans explicit capacity controls of a regularization term or constraint on the norm of the weights, to the mathematical computation that shows the unit vector (computed from the solution of gradient descent) remains the same, whether or not the constraint is enforced during gradient descent. In other words, deep networks select minimum norm solutions, hence the gradient flow of deep networks with an exponential-type loss locally minimizes the expected error. A New AI Study May Explain Why Deep Learning Works MIT researchers’ new theory illuminates machine learning’s black box.| Cami Rosso - Psychology Today ..PNAS (Proceedings of the National Academy of Sciences of the United States of America) | T. Poggio, A. Banburski, and Q. Liao
Opening the Black Box
- Opening the Black Box of Deep Neural Networks via Information | Ravid Schwartz-Ziv and Naftali Tishby - The Hebrew University of Jerusalem
- New Theory Cracks Open the Black Box of Deep Learning | Natalie Wolchover - QuantaMagazine

Decoding the Human Mind
Neural Network History
The history of neural networks is long and complex, but it can be traced back to the early days of artificial intelligence research. In 1943, Warren McCulloch and Walter Pitts published a paper in which they proposed a mathematical model of the human brain. This model, which was based on the idea that neurons in the brain are connected to each other, became the foundation for modern neural networks.

The inventors of the neural network Walter Pitts and Warren McCulloch pictured here in 1949. Semantic Scholar
In the 1950s, neural networks began to be used to solve real-world problems. One of the most famous early applications was the development of the Perceptron by Frank Rosenblatt in 1958. The Perceptron was a simple neural network that could be used to classify data. It was initially very successful, but it was later shown to be limited in its capabilities.
In the 1960s and 1970s, neural networks fell out of favor as researchers focused on other approaches to artificial intelligence. However, in the 1980s, there was a resurgence of interest in neural networks. This was due in part to the development of new algorithms that made neural networks more powerful.
In the 1990s, neural networks began to be used to solve a wide range of problems, including image recognition, speech recognition, and natural language processing. This was due in part to the availability of large amounts of data that could be used to train neural networks. There were many major contributors to neural networks in the 1990s. Some of the most notable include:
- Geoffrey Hinton, developed backpropagation, a technique for training neural networks that is still used today.
- Yann LeCun, developed convolutional neural networks, which are now widely used in image recognition and natural language processing.
- Yoshua Benigo, developed recurrent neural networks, which are used in tasks such as speech recognition and machine translation.
- Michael Jordan, work on theoretical insights into neural networks and their applications.
- Terrence Sejnowski, developed new learning algorithms and models, and applying neural networks to a variety of problems in machine learning and neuroscience.
In the 2000s, neural networks have become even more powerful due to the development of deep learning. Deep learning is a type of neural network that uses multiple layers of artificial neurons. Deep learning has been used to achieve state-of-the-art results on a wide range of problems, including image recognition, speech recognition, and natural language processing.
Today, neural networks are one of the most important tools in artificial intelligence. They are used in a wide range of applications, including self-driving cars, facial recognition, and fraud detection.
____________
David Rumelhart, who had a background in psychology and was a co-author of a set of books published in 1986 that would later drive attention back again towards neural networks, found himself collaborating on the development of neural networks with his colleague Jay McClelland. As well as being colleagues they had also recently encountered each other at a conference in Minnesota where Rumelhart’s talk on “story understanding” had provoked some discussion among the delegates. Following that conference McClelland returned with a thought about how to develop a neural network that might combine models to be more interactive. What matters here is Rumelhart’s recollection of the “hours and hours and hours of tinkering on the computer”...
We sat down and did all this in the computer and built these computer models, and we just didn’t understand them. We didn’t understand why they worked or why they didn’t work or what was critical about them.