Manifold Hypothesis
Youtube search... ...Google search
- Backpropagation ... FFNN ... Forward-Forward ... Activation Functions ...Softmax ... Loss ... Boosting ... Gradient Descent ... Hyperparameter ... Manifold Hypothesis ... PCA
- Embedding ... Fine-tuning ... RAG ... Search ... Clustering ... Recommendation ... Anomaly Detection ... Classification ... Dimensional Reduction. ...find outliers
- Objective vs. Cost vs. Loss vs. Error Function
- Optimization Methods
- Embedding ... Fine-tuning ... RAG ... Search ... Clustering ... Recommendation ... Anomaly Detection ... Classification ... Dimensional Reduction. ...find outliers
- Manifold Wikipedia
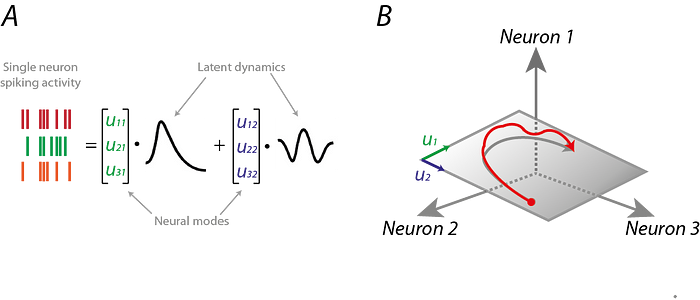
- Manifolds and Neural Activity: An Introduction | Kevin Luxem - Towards Data Science
The Manifold Hypothesis states that real-world high-dimensional data (images, neural activity) lie on low-dimensional manifolds
manifolds embedded within the high-dimensional space. ...manifolds are topological spaces that look locally like Euclidean spaces.
The Manifold Hypothesis explains (heuristically) why machine learning techniques are able to find useful features and produce accurate predictions from datasets that have a potentially large number of dimensions ( variables). The fact that the actual data set of interest actually lives on in a space of low dimension, means that a given machine learning model only needs to learn to focus on a few key features of the dataset to make decisions. However these key features may turn out to be complicated functions of the original variables. Many of the algorithms behind machine learning techniques focus on ways to determine these (embedding) functions. What is the Manifold Hypothesis? | DeepAI
|
|
Contents
What is a Manifold?
Manifolds are a complex topic, but they are very important in mathematics and physics. By understanding manifolds, we can better understand the world around us. A manifold is a curved surface that looks like a flat plane when you zoom in. For example, the surface of a sphere is a manifold. It looks curved from a distance, but if you look at a small enough patch of the sphere, it looks flat. Manifolds are important in mathematics and physics because they allow us to describe curved surfaces using flat geometry. This is useful because flat geometry is much simpler to understand than curved geometry.
For example, we can use manifolds to describe the space around us. Even though the space around us is curved, we can describe it using flat geometry by breaking it up into a bunch of small patches. Each patch is a manifold, and we can use flat geometry to describe each patch.
Manifolds are also important in relativity. Relativity is a theory of physics that describes space and time. In relativity, space and time are combined into a four-dimensional manifold.
This manifold is curved, but we can use flat geometry to describe it by breaking it up into a bunch of small patches. Each patch is a manifold, and we can use flat geometry to describe each patch. Here is a simple analogy to help you understand manifolds:
- Imagine you have a map of the world. The map is flat, but the Earth is a sphere. This means that the map is distorted. For example, Greenland appears to be larger than Africa on a map, but in reality Africa is much larger.
- A manifold is like a way to unfold the map so that it accurately represents the surface of the Earth. This would allow you to compare the distances between different places on the Earth more accurately.
Manifold Learning
Manifold learning is an approach to non-linear dimensionality reduction. Algorithms for this task are based on the idea that the dimensionality of many data sets is only artificially high. Manifold learning | SciKitLearn
Manifold learning is based on the assumption that many high-dimensional datasets lie on a low-dimensional manifold, which is a curved surface that is embedded in a higher-dimensional space. It is particularly useful for datasets that lie on a low-dimensional manifold, even if the manifold is non-linear. Manifold learning algorithms aim to find a low-dimensional embedding of the data that preserves the intrinsic geometry of the manifold. This can be useful for visualization, data analysis, and machine learning tasks. Some popular manifold learning algorithms include:
- Local Linear Embedding (LLE): LLE constructs a local linear model for each data point and then finds a low-dimensional embedding that preserves the local structure of the data.
- Isomap: Isomap constructs a graph of the data points based on their pairwise distances and then uses multidimensional scaling (MDS) to find a low-dimensional embedding of the graph.
- T-Distributed Stochastic Neighbor Embedding (t-SNE): t-SNE uses a probabilistic approach to find a [[Dimensional Reduction|low-dimensional] embedding of the data that preserves the local and global structure of the data.
Manifold learning algorithms have been used in a wide variety of applications, including:
- Image processing: Manifold learning can be used to reduce the dimensionality of images without losing important information. This can be useful for image compression, classification, and retrieval.
- Natural Language Processing (NLP): Manifold learning can be used to reduce the dimensionality of text data without losing important information. This can be useful for text classification, clustering, and machine translation.
- Bioinformatics: Manifold learning can be used to reduce the dimensionality of biological data, such as gene expression data and protein structure data. This can be useful for identifying disease biomarkers and developing new drugs.
Manifold Alignment
Imagine you have two different datasets, one of images of cats and one of images of dogs. Both datasets are high-dimensional, meaning that each image is represented by a long list of numbers.
Manifold alignment is a technique that can be used to find a common representation of these two datasets, even though they are different. It does this by assuming that the two datasets lie on a common manifold.
A manifold is a curved surface that locally resembles a flat plane. For example, the Earth's surface is a manifold. It is curved, but if you look at a small enough patch, it looks flat.
Manifold alignment works by finding a projection from each dataset to the manifold. This projection maps each image to a point on the manifold. The goal is to find projections that preserve the relationships between the images in each dataset.
Once the projections have been found, the two datasets can be represented in the same space. This makes it possible to compare the images in the two datasets directly.
For example, manifold alignment could be used to develop a system that can identify cats and dogs in images, even if the images are taken from different angles or in different lighting conditions.
Here is a simple analogy to help you understand manifold alignment:
Imagine you have a map of the world. The map is flat, but the Earth is a sphere. This means that the map is distorted. For example, Greenland appears to be larger than Africa on a map, but in reality Africa is much larger.
Manifold alignment is like finding a way to unfold the map so that it accurately represents the surface of the Earth. This would allow you to compare the distances between different places on the Earth more accurately.
Manifold alignment is a powerful technique that can be used to solve a variety of problems in machine learning. It is often used in applications such as image recognition, natural language processing, and data visualization.
Manifold - Defenses Against Adversarial Attacks
An adversarial example is a specially crafted input that is designed to fool a machine learning model. Adversarial examples are often created by adding small perturbations to normal inputs. These perturbations are imperceptible to humans, but they can cause the model to make incorrect predictions.
The manifold of normal examples is a mathematical object that represents the set of all normal inputs. It is a curved surface, and each normal input corresponds to a point on the manifold.
The reformer network is a type of neural network that can be used to defend against adversarial attacks. It works by moving adversarial examples towards the manifold of normal examples. This makes it more likely that the model will classify the adversarial examples correctly.
To understand how the reformer network works, it is helpful to think about an analogy. Imagine that the manifold of normal examples is a mountain range. The reformer network is like a force that pushes adversarial examples uphill, towards the highest peaks of the mountain range. The higher up the mountain an adversarial example is, the more likely it is to be classified correctly.
The reformer network is effective for correctly classifying adversarial examples with small perturbation because it moves the adversarial examples towards the manifold of normal examples. This makes it more likely that the model will classify the adversarial examples correctly.
Here is a concrete example of how the reformer network could be used to defend against an adversarial attack on an image classification model:
Suppose an attacker creates an adversarial image of a cat that is classified as a dog by the model. The reformer network could be used to move the adversarial image towards the manifold of normal images of cats. This would make it more likely that the model will classify the adversarial image correctly, as a cat.
The reformer network is a promising new defense against adversarial attacks. It is still under development, but it has shown promising results in experiments.
Einstein Manifolds
Einstein manifolds are special types of curved surfaces that are important in the theory of general relativity. General relativity is a theory of gravity that describes space and time as a curved four-dimensional surface. Einstein manifolds are surfaces that satisfy the Einstein field equations, which are the equations that govern gravity.
One way to think about Einstein manifolds is to imagine a trampoline with a bowling ball in the middle. The bowling ball will cause the trampoline to bend. This is similar to how gravity causes spacetime to bend.
If you roll a marble across the trampoline, it will follow a curved path. This is because the marble is following the curvature of the trampoline. In the same way, objects in spacetime follow curved paths because of the curvature of spacetime.
Einstein manifolds are mathematical models of bent spacetime. By studying Einstein manifolds, we can learn more about the nature of gravity and the structure of the universe.
Here is a simpler analogy:
Imagine you have a piece of paper. You can draw a straight line on the paper. This is like a flat surface.
Now, imagine you crumple the piece of paper into a ball. You can still draw a line on the paper, but it will be curved. This is like a curved surface.
Einstein manifolds are like curved surfaces, but they are four-dimensional. This means that they have four directions, instead of just two.
Einstein manifolds are important because they are models of the spacetime in which we live. Spacetime is the fabric of the universe, and it is curved because of gravity. By studying Einstein manifolds, we can learn more about the nature of gravity and how it works.