Kernel Trick

YouTube search... ...Google search

• Math for Intelligence ... Finding Paul Revere ... Social Network Analysis (SNA) ... Dot Product ... Kernel Trick
• AI Solver ... Algorithms ... Administration ... Model Search ... Discriminative vs. Generative ... Train, Validate, and Test
• Embedding ... Fine-tuning ... RAG ... Search ... Clustering ... Recommendation ... Anomaly Detection ... Classification ... Dimensional Reduction. ...find outliers
• Dimensional Reduction Algorithms
• Backpropagation ... FFNN ... Forward-Forward ... Activation Functions ...Softmax ... Loss ... Boosting ... Gradient Descent ... Hyperparameter ... Manifold Hypothesis ... PCA
  • T-Distributed Stochastic Neighbor Embedding (t-SNE)
  • Isomap
  • Local Linear Embedding (LLE)
• Perspective ... Context ... In-Context Learning (ICL) ... Transfer Learning ... Out-of-Distribution (OOD) Generalization
• Causation vs. Correlation ... Autocorrelation ...Convolution vs. Cross-Correlation (Autocorrelation)
• The Kernel Trick in Support Vector Classification | Drew Wilimitis
• Kernel Functions For Machine Learning | Prateek Joshi
• Kernel method | Wikipedia
• Efficient karaoke song recommendation via multiple kernel learning approximation | C. Guana, Y. Fub, X. Luc, E. Chena, X. Li, and H. Xiong

The word "kernel" is used in mathematics to denote a weighting function for a weighted sum or integral.

• formalizes a notion of similarity k(x, x') | Boser, Guyon, and Vapnik 1992
• induces a linear representation of the data in a vector space - no matter where the original data comes from | Scholkopf 1997
• encodes the function class used for learning - solutions of kernel algorithms can be expressed as kernel expansions | Kimeldorf, Wabba 1971, Scholkopf, Herbrich, and Smola 2001

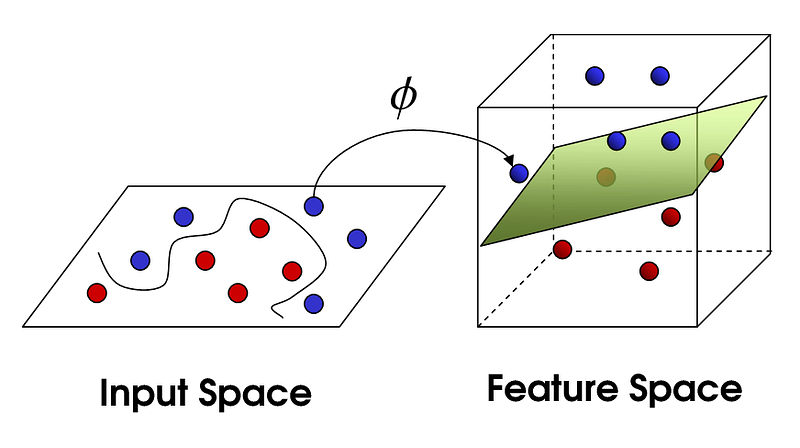
The 'Kernel Trick' avoids the explicit mapping that is needed to get linear learning algorithms to learn a nonlinear function or decision boundary.

Mathematical tool which can be applied to any algorithm which solely depends on the dot product between two vectors. Now where did Dot Product come from? When we want to transform data into higher dimensions, we cannot just randomly project it. We don’t want to compute the mapping explicitly either. Hence we use only those algorithms which use Dot Products of vectors in the higher dimension to come up with the boundary. This Dot Product corresponds to the mathematical processing step. To compute the Dot Products of vectors in the higher dimension, we don’t actually have to project the data into higher dimensions. We can use a kernel function to compute the Dot Product directly using the lower dimension vectors.

Kernel Approximation

functions that approximate the feature mappings that correspond to certain kernels, as they are used for example in Support Vector Machine (SVM). The feature functions perform non-linear transformations of the input, which can serve as a basis for linear classification or other algorithms. The advantage of using approximate explicit feature maps compared to the kernel trick, which makes use of feature maps implicitly, is that explicit mappings can be better suited for online learning and can significantly reduce the cost of learning with very large datasets. Standard kernelized Support Vector Machine (SVM)s do not scale well to large datasets, but using an approximate kernel map it is possible to use much more efficient linear Support Vector Machine (SVM)s. Kernel Approximation | Scikit-Learn