Hierarchical Clustering; Agglomerative (HAC) & Divisive (HDC)
Youtube search... ...Google search
- AI Solver ... Algorithms ... Administration ... Model Search ... Discriminative vs. Generative ... Train, Validate, and Test
- Embedding ... Fine-tuning ... RAG ... Search ... Clustering ... Recommendation ... Anomaly Detection ... Classification ... Dimensional Reduction. ...find outliers
- Hierarchical Cluster Analysis (HCA)
- Hierarchical Temporal Memory (HTM)
- K-Means
- How to Perform Hierarchical Clustering using R | Perceptive Analytics
- Exploreing K-Means with Internal Validity Indexes for Data Clustering in Traffic Management System | S. Nawrin, S. Akhter and M. Rahatur
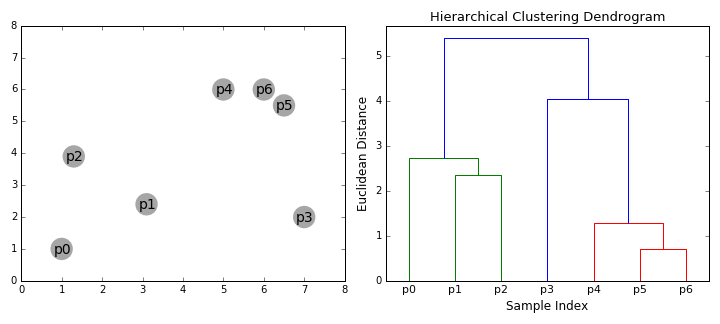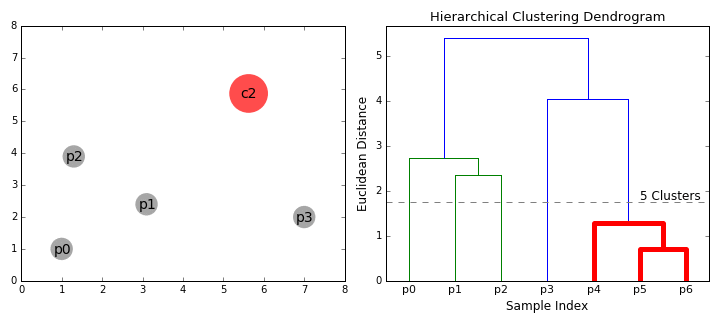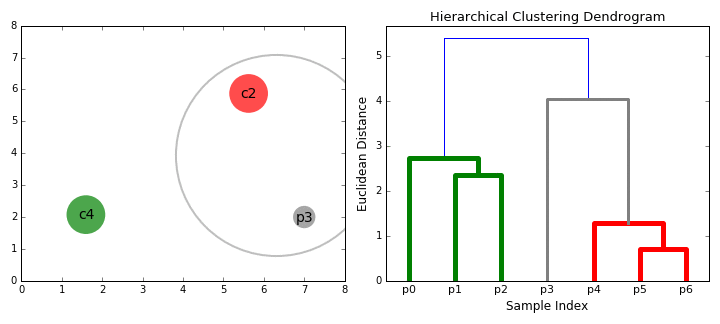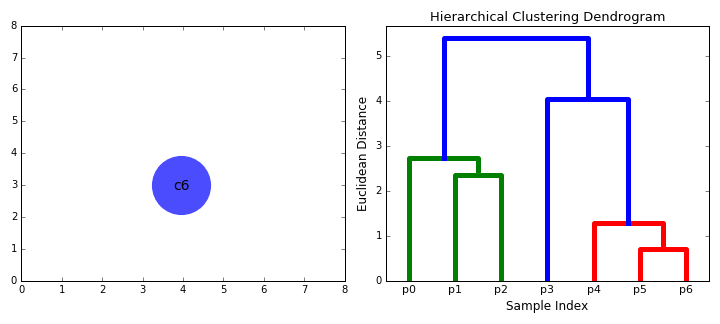
Hierarchical clustering algorithms actually fall into 2 categories:
- Agglomerative (HAC - AGNES); bottom-up, first assigns every example to its own cluster, and iteratively merges the closest clusters to create a hierarchical tree.
- Divisive (HDC - DIANA); top-down, first groups all examples into one cluster and then iteratively divides the cluster into a hierarchical tree.

Agglomerative Clustering - Bottom UpBottom-up algorithms treat each data point as a single cluster at the outset and then successively merge (or agglomerate) pairs of clusters until all clusters have been merged into a single cluster that contains all data points. Bottom-up hierarchical clustering is therefore called hierarchical agglomerative clustering or HAC. This hierarchy of clusters is represented as a tree (or dendrogram). The root of the tree is the unique cluster that gathers all the samples, the leaves being the clusters with only one sample. The 5 Clustering Algorithms Data Scientists Need to Know | Towards Data Science Hierarchical clustering does not require us to specify the number of clusters and we can even select which number of clusters looks best since we are building a tree. Additionally, the algorithm is not sensitive to the choice of distance metric; all of them tend to work equally well whereas with other clustering algorithms, the choice of distance metric is critical. A particularly good use case of hierarchical clustering methods is when the underlying data has a hierarchical structure and you want to recover the hierarchy; other clustering algorithms can’t do this. These advantages of hierarchical clustering come at the cost of lower efficiency, as it has a time complexity of O(n³), unlike the linear complexity of K-Means and GMM.
Divisive Clustering = Top Down
|