Difference between revisions of "Dot Product"
m |
m (Text replacement - "http:" to "https:") |
||
| Line 15: | Line 15: | ||
* [[Kernel Trick]] | * [[Kernel Trick]] | ||
* [[Math for Intelligence]] | * [[Math for Intelligence]] | ||
| − | * [ | + | * [https://en.wikipedia.org/wiki/Dot_product Dot Product | Wikipedia] |
Dot Product = | Dot Product = | ||
| Line 21: | Line 21: | ||
* Geometrically, it is the product of the Euclidean magnitudes of the two vectors and the cosine of the angle between them. | * Geometrically, it is the product of the Euclidean magnitudes of the two vectors and the cosine of the angle between them. | ||
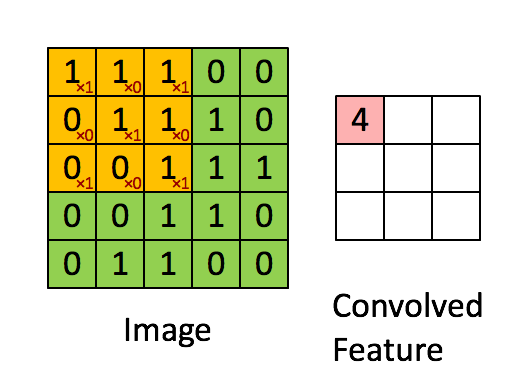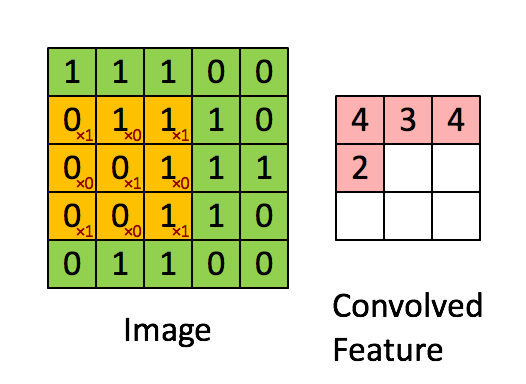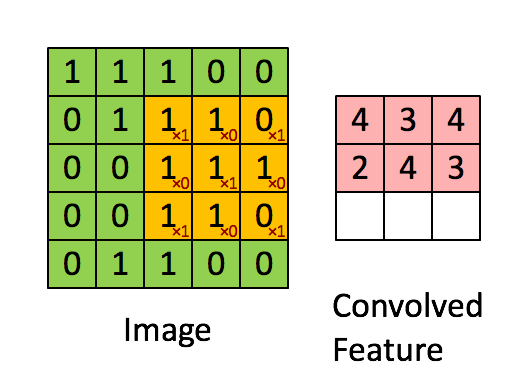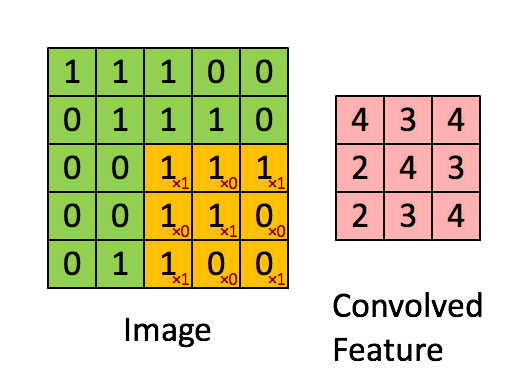
| − | + | https://ujwlkarn.files.wordpress.com/2016/07/convolution_schematic.gif | |
| − | [ | + | [https://ujjwalkarn.me/2016/08/11/intuitive-explanation-convnets/ Take a moment to understand how the computation above is being done. We slide the orange matrix over our original image (green) by 1 pixel (also called ‘stride’) and for every position, we compute element wise multiplication (between the two matrices) and add the multiplication outputs to get the final integer which forms a single element of the output matrix (pink). Note that the 3×3 matrix “sees” only a part of the input image in each stride. In CNN terminology, the 3×3 matrix is called a ‘filter‘ or ‘kernel’ or ‘feature detector’ and the matrix formed by sliding the filter over the image and computing the dot product is called the ‘Convolved Feature’ or ‘Activation Map’ or the ‘Feature Map‘. It is important to note that filters acts as feature detectors from the original input image. | ujjwalkarn] |
| − | + | https://upload.wikimedia.org/wikipedia/commons/thumb/e/eb/Matrix_multiplication_diagram_2.svg/313px-Matrix_multiplication_diagram_2.svg.png | |
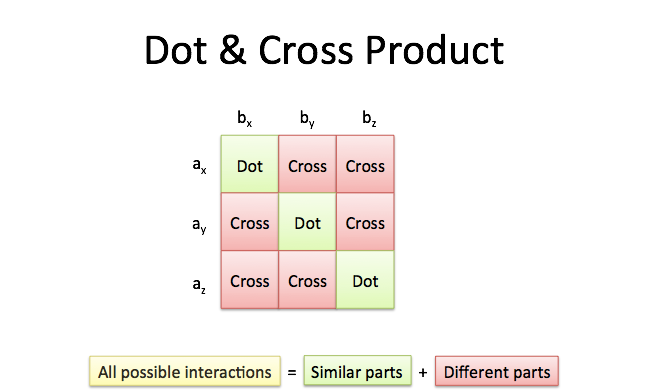
| − | + | https://betterexplained.com/wp-content/uploads/crossproduct/cross-product-grid.png | |
Revision as of 10:04, 28 March 2023
YouTube ... Quora ...Google search ...Google News ...Bing News
Dot Product =
- Algebraically, the dot product is the sum of the products of the corresponding entries of the two sequences of numbers.
- Geometrically, it is the product of the Euclidean magnitudes of the two vectors and the cosine of the angle between them.