Activation Functions

From
Revision as of 08:16, 6 August 2023 by BPeat (talk | contribs)
Jump to: navigation, search

YouTube Search] ...Google search


Activation functions are the mathematical gates that determine, at each node in a Neural Network, whether and to what extent to transmit the signal the node has received from the previous layer.

A combination of weights (coefficients) and biases work on the input data from the previous layer to determine whether that signal surpasses a given threshold and is deemed significant. Those weights and biases are slowly updated as the neural net minimizes its error; i.e. the level of nodes’ activation change in the course of learning. They introduce non-linearity into the network, allowing it to learn and approximate complex relationships between inputs and outputs. Activation functions/gates are an essential component of Deep Learning models and are applied at each layer of the Neural Network. The choice of activation function/gate depends on the problem requirements and the characteristics of the data being processed. Different activation functions/gates offer distinct properties and advantages, and researchers continue to explore new variations to improve the performance and efficiency of deep learning models.


When we learn something new, like reading a story, our brain sends signals to tell us how much we should focus on that information. Without activation functions/gates, the AI will get overwhelmed with all the data it gets and not know what to do. Activation functions/gates helps the AI make better decisions, learn from its experiences, and improve its skills.



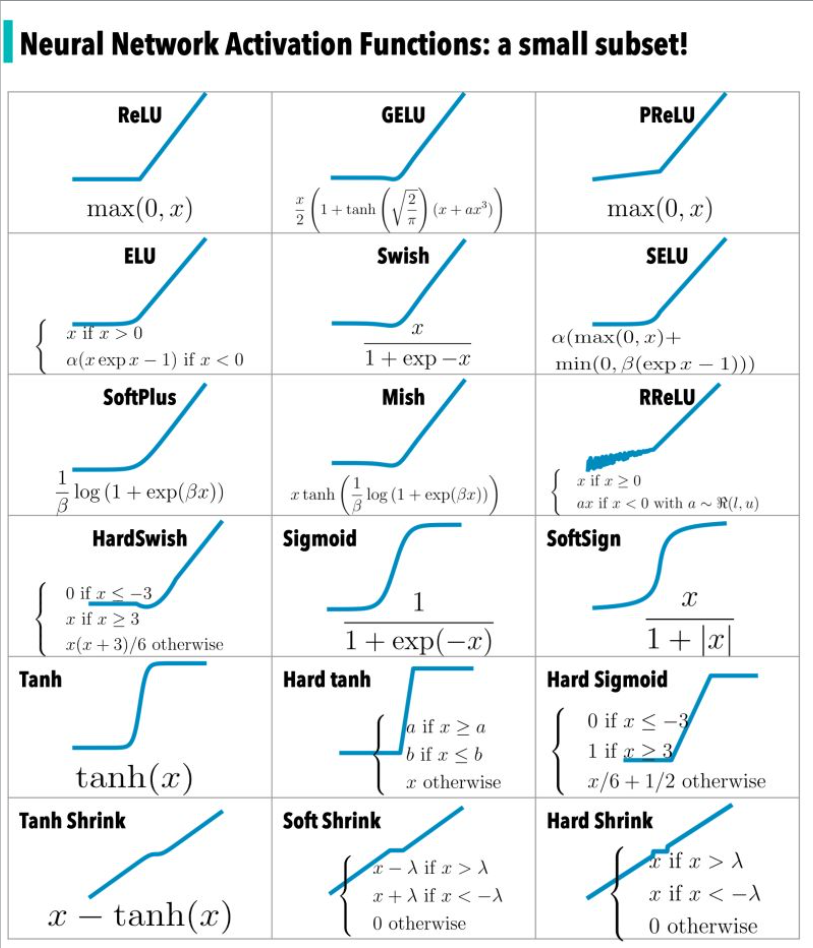
Types of Activation Functions/Gates

There are several types of activation functions/gates commonly used in AI:

  • Step Function: The step function is a simple activation function that maps input values below a threshold to 0 and values above the threshold to 1. It is not commonly used in deep learning due to its discontinuous nature, which makes it challenging to optimize during training.
  • Linear Function: The linear activation function computes the weighted sum of the inputs without applying any non-linearity. It is primarily used in linear regression models or as the output layer activation function in certain cases.
  • Sigmoid Function: The sigmoid function, also known as the logistic function, maps the input to a smooth S-shaped curve between 0 and 1. It is widely used as an activation function in the hidden layers of neural networks for binary classification problems. The sigmoid function squashes the output of a neuron to a range suitable for probability interpretation.
  • Tanh Function: The hyperbolic tangent (tanh) function is similar to the sigmoid function but maps the input to a range between -1 and 1. It exhibits stronger non-linearity compared to the sigmoid function and is often used in recurrent neural networks (RNNs) and hidden layers of feedforward neural networks.
  • Rectified Linear Unit (ReLU): The rectified linear unit (ReLU) is one of the most widely used activation functions. It returns the input as the output if it is positive, and 0 otherwise. ReLU introduces non-linearity and overcomes the vanishing gradient problem, making it efficient and effective for training deep neural networks.
  • Leaky ReLU: The leaky ReLU is a variation of the ReLU function that allows a small, non-zero gradient when the input is negative. This modification addresses the "dying ReLU" problem where a neuron can become inactive and stop learning.
  • Exponential Linear Unit (ELU): The exponential linear unit (ELU) function is similar to the leaky ReLU but has a negative output when the input is less than zero. ELU helps improve the robustness of the model to noise and can lead to better generalization.



'https://miro.medium.com/max/1280/1*xYCVODGB7RwJ9RynebB2qw.gif'

'https://miro.medium.com/max/1200/1*HBvDu4Rl56AEz_jvF3BYBQ.gif'


Why Non-linear Activation Functions are Preferred Over Linear Functions

Non-linear Activation Functions is essential because they enable AI models to handle complex problems, learn hierarchical representations, and approximate a wide range of functions. They provide the flexibility and power needed to build sophisticated AI systems that can tackle real-world challenges effectively.

  • Enabling Complexity: Non-linear Activation Functions introduce non-linearities into the AI model, which allows it to capture and represent complex relationships between input data and output predictions. Many real-world problems are inherently non-linear, and using linear Activation Functions would limit the AI model's ability to handle these complexities effectively.
  • Universal Approximation Theorem: One of the fascinating properties of non-linear Activation Functions is that they can approximate any continuous function, given the right parameters. This property is called the Universal Approximation Theorem. It means that by using non-linear Activation Functions, we can build AI models that are capable of approximating almost any function, making them more versatile and adaptable.
  • Learning Hierarchies: Deep learning, a subfield of AI, has become very successful due to the use of deep neural networks with multiple layers. Non-linear Activation Functions play a crucial role in this success. With each layer using non-linearities, the AI model can learn hierarchical representations of the data, capturing abstract features at higher layers and building a rich understanding of the input.
  • Avoiding Vanishing and Exploding Gradients: Linear Activation Functions suffer from vanishing and exploding gradient problems. When gradients become too small (vanish) or too large (explode), it becomes difficult for the AI model to learn effectively. Non-linear Activation Functions help mitigate these issues, making the training process more stable and efficient.
  • Better Decision Boundaries: In classification tasks, AI models with non-linear Activation Functions can create more complex decision boundaries, allowing them to distinguish between classes more accurately. Linear Activation Functions would only allow for linear decision boundaries, limiting the model's ability to handle complex data distributions.


Choosing Activation Functions

The choice of activation function depends on the problem at hand and the characteristics of the data. Some guidelines for selecting activation functions include:

  • For binary classification problems, sigmoid or tanh functions are often used in the hidden layers, while sigmoid or softmax functions are used in the output layer.
  • ReLU and its variants (leaky ReLU, ELU) are commonly employed in the hidden layers of deep neural networks due to their computational efficiency and ability to prevent the vanishing gradient problem.
  • It is important to consider the properties of the activation function, such as differentiability, monotonicity, and range of output values, to ensure compatibility with the optimization algorithms and desired behavior of the network.


Begin with using ReLU function and then move over to other activation functions in case ReLU doesn’t provide with optimum results. (Always keep in mind that ReLU function should only be used in the hidden layers.)


'https://aman.ai/primers/ai/assets/activation/1.png'



Threshold (binary step)

More theoretical than practical; e.g. not offered in TensorFlow library. the gradient of the step function is zero. This makes the step function not so useful since during back-propagation when the gradients of the activation functions are sent for error calculations to improve and optimize the results. The gradient of the step function reduces it all to zero and improvement of the models doesn’t really happen.


Identity (linear)

This can be applied to various neurons and multiple neurons can be activated at the same time. Now, when we have multiple classes, we can choose the one which has the maximum value. The derivative of a linear function is constant i.e. it does not depend upon the input value x. This means that every time we do a back propagation, the gradient would be the same.

Sigmoid (logistic)

A smooth function and is continuously differentiable with the result existing between (0 to 1). Therefore, it is especially used for models where we have to predict the probability as an output - anything exists only between the range of 0 and 1. Has vanishing gradient problem.


tanh (hyperbolic tangent)

The range of the tanh function is from (-1 to 1) - offset of Sigmoid to be zero centered. tanh is also s - shaped. Solves our problem of the values all being of the same sign. Has vanishing gradient problem.


ReLU (Rectified Linear Unit)

half rectified (from bottom). f(z) is zero when z is less than zero and f(z) is equal to z when z is above or equal to zero. The main advantage of using the ReLU function over other activation functions is that it does not activate all the neurons at the same time. What does this mean ? If you look at the ReLU function if the input is negative it will convert it to zero and the neuron does not get activated. This means that at a time only a few neurons are activated making the network sparse making it efficient and easy for computation. The ReLU is the most used activation function in the world right now.But ReLU also falls a prey to the gradients moving towards zero. If you look at the negative side of the graph, the gradient is zero, which means for activations in that region, the gradient is zero and the weights are not updated during back propagation. This can create dead neurons which never get activated.

Leaky ReLU (Rectified Linear Unit)

in an attempt to solve the dying ReLU problem, instead of defining the Relu function as 0 for x less than 0, we define it as a small linear component of x. The main advantage of replacing the horizontal line is to remove the zero gradient.

Explained

Parameterised ReLU (Rectified Linear Unit)

Similar to the Leaky ReLU function that has trainable parameter resulting in learning the value of ‘a‘ for faster and more optimum convergence. The parametrised ReLU function is used when the leaky ReLU function still fails to solve the problem of dead neurons and the relevant information is not successfully passed to the next layer.

Keras - Advanced Activation Layers

Softmax

  • Softmax - visit page for more information

Squeezes the outputs for each class between 0 and 1 and would also divide by the sum of the outputs. This essentially gives the probability of the input being in a particular class.

Neural Arithmetic Logic Units (NALU)

Neural networks can learn to represent and manipulate numerical information, but they seldom generalize well outside of the range of numerical values encountered during training. To encourage more systematic numerical extrapolation, we propose an architecture that represents numerical quantities as linear activations which are manipulated using primitive arithmetic operators, controlled by learned gates. We call this module a neural arithmetic logic unit (NALU), by analogy to the arithmetic logic unit in traditional processors. Experiments show that NALU-enhanced neural networks can learn to track time, perform arithmetic over images of numbers, translate numerical language into real-valued scalars, execute computer code, and count objects in images. In contrast to conventional architectures, we obtain substantially better generalization both inside and outside of the range of numerical values encountered during training, often extrapolating orders of magnitude beyond trained numerical ranges.

______________________________________________________________

The activation functions provide different types of nonlinearities for use in neural networks. These include smooth nonlinearities (sigmoid, tanh, elu, selu, softplus, and softsign), continuous but not everywhere differentiable functions (relu, relu6, crelu and relu_x), and random regularization (dropout). All activation ops apply componentwise, and produce a tensor of the same shape as the input tensor.

Weights

Weights determine the strength of the connections between neurons in different layers of the network, enabling the network to adjust and adapt during the learning process. Weights and activation functions work together in Neural Networks.

Weights in Neural Networks

  • In a neural network, each connection between neurons is associated with a weight. These weights represent the strength of the connection between two neurons and act as parameters that the network adjusts during training to optimize its performance.
  • Initially, the weights in a neural network are assigned random values. As the network is trained on a labeled dataset, these weights are updated using optimization algorithms like gradient descent, which minimizes the error between the network's predicted output and the actual output.
  • The weights determine the contribution of each neuron's output to the input of the subsequent neurons in the network. A larger weight implies a stronger influence, while a smaller weight implies a weaker influence.
  • During training, the network adjusts the weights based on the error signal propagated through the network. This adjustment aims to minimize the overall error and improve the network's ability to make accurate predictions.
  • The final values of the weights after training represent the learned patterns and relationships in the input data, which the network can utilize to make predictions on unseen data.

Interaction between Weights and Activation Functions

  • Weights and activation functions work together in a neural network. The weights determine the strength of the connections between neurons, while the activation functions introduce non-linearity to capture complex patterns in the data.
  • The weights are responsible for controlling the contribution of each neuron's output to the subsequent layers. By adjusting the weights, the network can assign more or less importance to certain features or patterns in the input data.
  • The activation functions, on the other hand, determine the output range and the transformation applied to the network's activations. The non-linear nature of the activation functions allows the network to model complex relationships and learn non-linear decision boundaries.
  • During the forward pass of training or inference, the activation of a neuron is computed by taking the weighted sum of inputs and passing it through the activation function. This transformed activation becomes the input for the next layer of neurons.
  • The weights are updated during the backward pass of training using gradient descent or other optimization algorithms. The updates are based on the gradients of the loss function with respect to the weights, which are obtained through backpropagation.
  • The combination of different weights and activation functions in the network architecture determines the overall learning capacity and flexibility of the neural network. Different choices of activation functions and weight initialization schemes can have a significant impact on the network's performance and convergence.

Vanishing & Exploding Gradients

A problem resulting from backpropagation.

Vanishing Gradients

The vanishing gradient is a problem that can occur during the training of artificial neural networks, especially in deep learning architectures. When a neural network has many layers, the gradients of the loss function with respect to the weights of the earlier layers can become extremely small (close to zero) as they propagate backward through the network during the training process.

Gradients represent how much the weights of the neural network should be adjusted to minimize the error (loss) during training. In other words, they show the direction and magnitude of the change needed to improve the model's predictions. However, if the gradients become too small, it means that the weights of the earlier layers are barely being updated, and these layers are not learning effectively.

This problem often arises when using certain activation functions, particularly in deep networks. For instance, the sigmoid activation function, which is an S-shaped curve, can cause the gradients to become very small for large or small input values. This effect gets compounded as the gradients are propagated through multiple layers, making the earlier layers learn very slowly or not at all.

When the vanishing gradient problem occurs, it can lead to slower convergence during training, and in extreme cases, the network may struggle to learn meaningful patterns from the data. This phenomenon hampers the ability of deep neural networks to effectively model complex relationships in the data, limiting their performance.


Exploding Gradients

The exploding gradient is another problem that can occur during the training of artificial neural networks, particularly in deep learning architectures. Unlike the vanishing gradient problem, where gradients become too small, the exploding gradient problem is when the gradients become too large.

During the training process, the gradients represent the direction and magnitude of the changes that need to be made to the model's weights to minimize the error (loss). When the gradients become very large, they can cause the weights to be updated by a significant amount, leading to unstable and erratic training behavior.

This problem often arises when there are very high values in the neural network, such as large weight values or input data with extreme magnitudes. As the gradients are propagated backward through the network, they can get amplified at each layer, resulting in explosive growth. This can lead to drastic weight updates and can make the model's training process highly unpredictable and difficult to converge.

When the exploding gradient problem occurs, it can lead to numerical instability during training. The model might experience "NaN" (not a number) values or overflow errors, which can prevent the training from proceeding correctly.

To mitigate the exploding gradient problem, several techniques have been developed. One common approach is gradient clipping, where the gradients are rescaled if they exceed a certain threshold. By capping the gradient magnitudes, the weight updates become more controlled, preventing them from growing too large and causing numerical issues.

Other methods, such as using weight initialization techniques that help control the magnitude of weights or employing gradient normalization techniques like gradient scaling, can also help stabilize training and address the exploding gradient problem.

Retrieved from "https://primo.ai/index.php?title=Activation_Functions&oldid=32787"