Difference between revisions of "Markov Decision Process (MDP)"
| Line 16: | Line 16: | ||
Solutions: | Solutions: | ||
* [http://www.google.com/search?q=Dynamic+Programming+reinforcement+learning&oq=Dynamic+Programming+reinforcement+learning Dynamic Programming] | * [http://www.google.com/search?q=Dynamic+Programming+reinforcement+learning&oq=Dynamic+Programming+reinforcement+learning Dynamic Programming] | ||
| − | * [ | + | * [[Monte Carlo]] |
* [http://www.google.com/search?ei=NJMKW97aLof_zgKM8KSgBA&q=Temporal+Difference+reinforcement+learning Difference Learning] | * [http://www.google.com/search?ei=NJMKW97aLof_zgKM8KSgBA&q=Temporal+Difference+reinforcement+learning Difference Learning] | ||
Revision as of 14:51, 11 August 2019
Youtube search... ...Google search

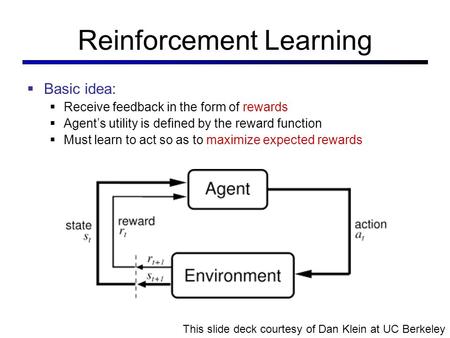
Solutions:
Used where outcomes are partly random and partly under the control of a decision maker. MDP is a discrete time stochastic control process. At each time step, the process is in some state s, and the decision maker may choose any action a that is available in state s. The process responds at the next time step by randomly moving into a new state s', and giving the decision maker a corresponding reward R_{a}(s,s')} R_a(s,s'). The probability that the process moves into its new state s' is influenced by the chosen action. Helping the convergence of certain algorithms a discount rate (factor) makes an infinite sum finite.