Difference between revisions of "Markov Decision Process (MDP)"
| Line 12: | Line 12: | ||
** [[Monte Carlo]] (MC) Method - Model Free Reinforcement Learning | ** [[Monte Carlo]] (MC) Method - Model Free Reinforcement Learning | ||
** Markov Decision Process (MDP) | ** Markov Decision Process (MDP) | ||
| + | ** [[State-Action-Reward-State-Action (SARSA)]] | ||
** [[Q Learning]] | ** [[Q Learning]] | ||
| − | ** [[ | + | *** [[Deep Q Network (DQN)]] |
** [[Deep Reinforcement Learning (DRL)]] DeepRL | ** [[Deep Reinforcement Learning (DRL)]] DeepRL | ||
** [[Distributed Deep Reinforcement Learning (DDRL)]] | ** [[Distributed Deep Reinforcement Learning (DDRL)]] | ||
| − | |||
** [[Evolutionary Computation / Genetic Algorithms]] | ** [[Evolutionary Computation / Genetic Algorithms]] | ||
** [[Actor Critic]] | ** [[Actor Critic]] | ||
Revision as of 06:06, 6 July 2020
Youtube search... ...Google search
- Markov Model (Chain, Discrete Time, Continuous Time, Hidden)
- Reinforcement Learning (RL)
- Monte Carlo (MC) Method - Model Free Reinforcement Learning
- Markov Decision Process (MDP)
- State-Action-Reward-State-Action (SARSA)
- Q Learning
- Deep Reinforcement Learning (DRL) DeepRL
- Distributed Deep Reinforcement Learning (DDRL)
- Evolutionary Computation / Genetic Algorithms
- Actor Critic
- Hierarchical Reinforcement Learning (HRL)

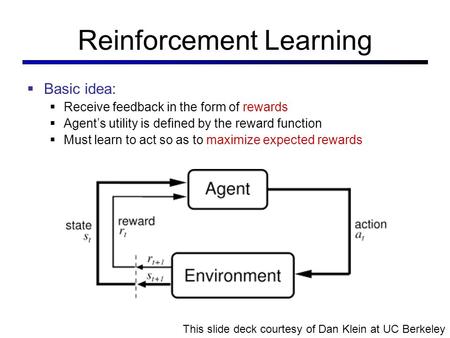
Solutions:
Used where outcomes are partly random and partly under the control of a decision maker. MDP is a discrete time stochastic control process. At each time step, the process is in some state s, and the decision maker may choose any action a that is available in state s. The process responds at the next time step by randomly moving into a new state s', and giving the decision maker a corresponding reward R_{a}(s,s')} R_a(s,s'). The probability that the process moves into its new state s' is influenced by the chosen action. Helping the convergence of certain algorithms a discount rate (factor) makes an infinite sum finite.