Gradient Descent Optimization & Challenges
YouTube search... ...Google search
- Backpropagation ... FFNN ... Forward-Forward ... Activation Functions ...Softmax ... Loss ... Boosting ... Gradient Descent ... Hyperparameter ... Manifold Hypothesis ... PCA
- Objective vs. Cost vs. Loss vs. Error Function
- Topology and Weight Evolving Artificial Neural Network (TWEANN)
- What is Gradient Descent? | Daniel Nelson - Unite.ai
- Other Challenges in Artificial Intelligence
- Average-Stochastic Gradient Descent (SGD) Weight-Dropped LSTM (AWD-LSTM)
- Optimization Methods
- Process Supervision
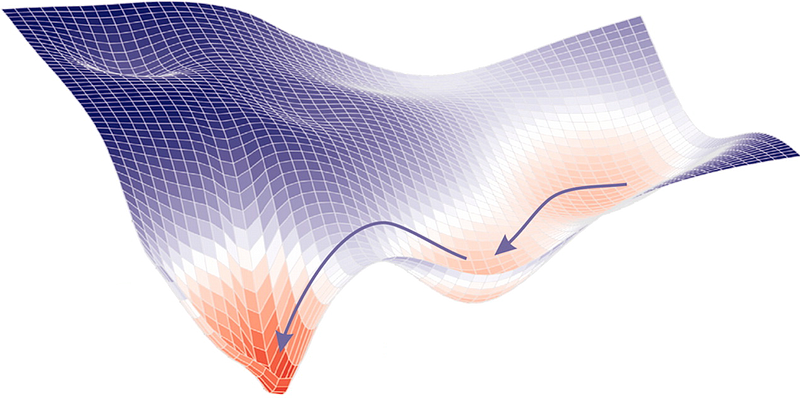
Gradient descent is an optimization algorithm used to minimize some function by iteratively moving in the direction of steepest descent as defined by the negative of the gradient. In machine learning, we use gradient descent to update the parameters of our model. Parameters refer to coefficients in Linear Regression and weights in neural networks. Gradient Descent | ML Cheatsheet
Gradient Descent is the most common optimization algorithm in machine learning and deep learning. It is a first-order optimization algorithm. This means it only takes into account the first derivative when performing the updates on the parameters. On each iteration, we update the parameters in the opposite direction of the gradient of the objective function J(w) w.r.t the parameters where the gradient gives the direction of the steepest ascent. Gradient Descent Algorithm and Its Variants | Imad Dabbura - Towards Data Science
Nonlinear Regression algorithms, which fit curves that are not linear in their parameters to data, are a little more complicated, because, unlike linear Regression problems, they can’t be solved with a deterministic method. Instead, the nonlinear Regression algorithms implement some kind of iterative minimization process, often some variation on the method of steepest descent. Steepest descent basically computes the squared error and its gradient at the current parameter values, picks a step size (aka learning rate), follows the direction of the gradient “down the hill,” and then recomputes the squared error and its gradient at the new parameter values. Eventually, with luck, the process converges. The variants on steepest descent try to improve the convergence properties. Machine learning algorithms are even less straightforward than nonlinear Regression, partly because machine learning dispenses with the constraint of fitting to a specific mathematical function, such as a polynomial. There are two major categories of problems that are often solved by machine learning: Regression and classification. Regression is for numeric data (e.g. What is the likely income for someone with a given address and profession?) and classification is for non-numeric data (e.g. Will the applicant default on this loan?). Machine learning algorithms explained | Martin Heller - InfoWorld
Contents
Gradient Descent - Stochastic (SGD), Batch (BGD) & Mini-Batch
Youtube search... ...Google search
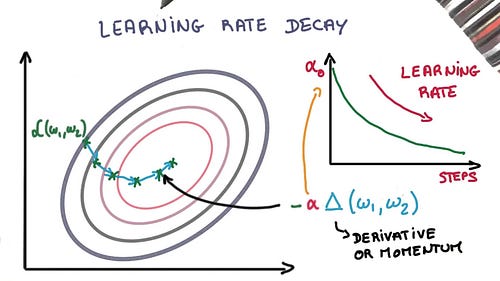
Learning Rate Decay
YouTube search... ...Google search
Adapting the learning rate for your stochastic gradient descent optimization procedure can increase performance and reduce training time. Sometimes this is called learning rate annealing or adaptive learning rates. The simplest and perhaps most used adaptation of learning rate during training are techniques that reduce the learning rate over time. These have the benefit of making large changes at the beginning of the training procedure when larger learning rate values are used, and decreasing the learning rate such that a smaller rate and therefore smaller training updates are made to weights later in the training procedure. This has the effect of quickly learning good weights early and fine tuning them later. The 10 Deep Learning Methods AI Practitioners Need to Apply | James Le
Two popular and easy to use learning rate decay are as follows:
- Decrease the learning rate gradually based on the epoch.
- Decrease the learning rate using punctuated large drops at specific epochs.
|
|
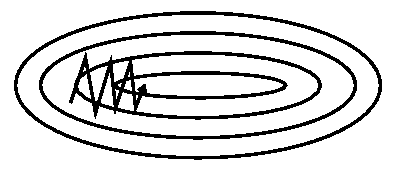
Gradient Descent With Momentum
YouTube search... ...Google search
helps accelerate gradients vectors in the right directions, thus leading to faster converging. It is one of the most popular optimization algorithms and many state-of-the-art models are trained using it... With Stochastic Gradient Descent we don’t compute the exact derivate of our loss function. Instead, we’re estimating it on a small batch. Which means we’re not always going in the optimal direction, because our derivatives are ‘noisy’. Just like in my graphs above. So, exponentially weighed averages can provide us a better estimate which is closer to the actual derivate than our noisy calculations. This is one reason why momentum might work better than classic SGD. The other reason lies in ravines. Ravine is an area, where the surface curves much more steeply in one dimension than in another. Ravines are common near local minimas in deep learning and SGD has troubles navigating them. SGD will tend to oscillate across the narrow ravine since the negative gradient will point down one of the steep sides rather than along the ravine towards the optimum. Momentum helps accelerate gradients in the right direction. This is expressed in the following pictures: Stochastic Gradient Descent with momentum | Vitaly Bushaev - Towards Data Science

|
|
Vanishing & Exploding Gradients
YouTube Search ...Google search
A problem resulting from backpropagation.
Vanishing Gradients
The vanishing gradient is a problem that can occur during the training of artificial neural networks, especially in deep learning architectures. When a neural network has many layers, the gradients of the loss function with respect to the weights of the earlier layers can become extremely small (close to zero) as they propagate backward through the network during the training process.
Gradients represent how much the weights of the neural network should be adjusted to minimize the error (loss) during training. In other words, they show the direction and magnitude of the change needed to improve the model's predictions. However, if the gradients become too small, it means that the weights of the earlier layers are barely being updated, and these layers are not learning effectively.
This problem often arises when using certain activation functions, particularly in deep networks. For instance, the sigmoid activation function, which is an S-shaped curve, can cause the gradients to become very small for large or small input values. This effect gets compounded as the gradients are propagated through multiple layers, making the earlier layers learn very slowly or not at all.
When the vanishing gradient problem occurs, it can lead to slower convergence during training, and in extreme cases, the network may struggle to learn meaningful patterns from the data. This phenomenon hampers the ability of deep neural networks to effectively model complex relationships in the data, limiting their performance.
Exploding Gradients
The exploding gradient is another problem that can occur during the training of artificial neural networks, particularly in deep learning architectures. Unlike the vanishing gradient problem, where gradients become too small, the exploding gradient problem is when the gradients become too large.
During the training process, the gradients represent the direction and magnitude of the changes that need to be made to the model's weights to minimize the error (loss). When the gradients become very large, they can cause the weights to be updated by a significant amount, leading to unstable and erratic training behavior.
This problem often arises when there are very high values in the neural network, such as large weight values or input data with extreme magnitudes. As the gradients are propagated backward through the network, they can get amplified at each layer, resulting in explosive growth. This can lead to drastic weight updates and can make the model's training process highly unpredictable and difficult to converge.
When the exploding gradient problem occurs, it can lead to numerical instability during training. The model might experience "NaN" (not a number) values or overflow errors, which can prevent the training from proceeding correctly.
To mitigate the exploding gradient problem, several techniques have been developed. One common approach is gradient clipping, where the gradients are rescaled if they exceed a certain threshold. By capping the gradient magnitudes, the weight updates become more controlled, preventing them from growing too large and causing numerical issues.
Other methods, such as using weight initialization techniques that help control the magnitude of weights or employing gradient normalization techniques like gradient scaling, can also help stabilize training and address the exploding gradient problem.
Vanishing & Exploding Gradients Challenges with Long Short-Term Memory (LSTM) and Recurrent Neural Networks (RNN)
YouTube Search ...Google search