Difference between revisions of "Ridge Regression"
| Line 9: | Line 9: | ||
* [[Logistic Regression (LR)]] | * [[Logistic Regression (LR)]] | ||
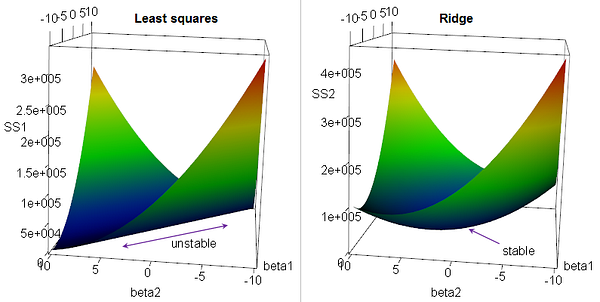
| − | + | or Tikhonov Regularization, is the most commonly used regression algorithm to approximate an answer for an equation with no unique solution. This type of problem is very common in machine learning tasks, where the "best" solution must be chosen using limited data. Simply, [Regularization]] introduces additional information to an problem to choose the "best" solution for it. This algorithm is used for analyzing multiple regression data that suffer from multicollinearity. Multicollinearity, or collinearity, is the existence of near-linear relationships among the independent variables. When multicollinearity occurs, least squares estimates are unbiased, but their variances are large so they may be far from the true value. By adding a degree of bias to the regression estimates, ridge regression reduces the standard errors. | |
http://cdn-images-1.medium.com/max/600/0*5hhRo51IxvuvU0TT.png | http://cdn-images-1.medium.com/max/600/0*5hhRo51IxvuvU0TT.png | ||
Revision as of 13:57, 7 January 2019
YouTube search... ...Google search
or Tikhonov Regularization, is the most commonly used regression algorithm to approximate an answer for an equation with no unique solution. This type of problem is very common in machine learning tasks, where the "best" solution must be chosen using limited data. Simply, [Regularization]] introduces additional information to an problem to choose the "best" solution for it. This algorithm is used for analyzing multiple regression data that suffer from multicollinearity. Multicollinearity, or collinearity, is the existence of near-linear relationships among the independent variables. When multicollinearity occurs, least squares estimates are unbiased, but their variances are large so they may be far from the true value. By adding a degree of bias to the regression estimates, ridge regression reduces the standard errors.