Difference between revisions of "Mean-Shift Clustering"
| Line 15: | Line 15: | ||
In contrast to K-means clustering there is no need to select the number of clusters as mean-shift automatically discovers this. That’s a massive advantage. The fact that the cluster centers converge towards the points of maximum density is also quite desirable as it is quite intuitive to understand and fits well in a naturally data-driven sense. The drawback is that the selection of the window size/radius “r” can be non-trivial. | In contrast to K-means clustering there is no need to select the number of clusters as mean-shift automatically discovers this. That’s a massive advantage. The fact that the cluster centers converge towards the points of maximum density is also quite desirable as it is quite intuitive to understand and fits well in a naturally data-driven sense. The drawback is that the selection of the window size/radius “r” can be non-trivial. | ||
| − | <youtube> | + | <youtube>M8B3RZVqgOo</youtube> |
| − | <youtube> | + | <youtube>TO8I-nggpzs</youtube> |
| − | <youtube> | + | <youtube>DEtx_R1NzPY</youtube> |
| − | <youtube> | + | <youtube>Evc53OaDTFc</youtube> |
Revision as of 20:12, 30 May 2018
Mean shift clustering is a sliding-window-based algorithm that attempts to find dense areas of data points. It is a centroid-based algorithm meaning that the goal is to locate the center points of each group/class, which works by updating candidates for center points to be the mean of the points within the sliding-window. These candidate windows are then filtered in a post-processing stage to eliminate near-duplicates, forming the final set of center points and their corresponding groups. The 5 Clustering Algorithms Data Scientists Need to Know | Towards Data Science
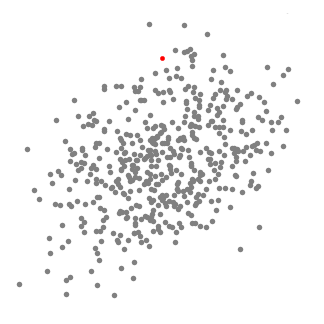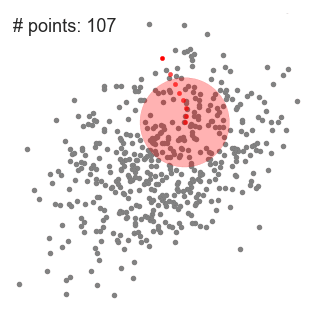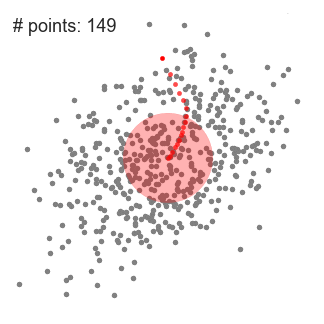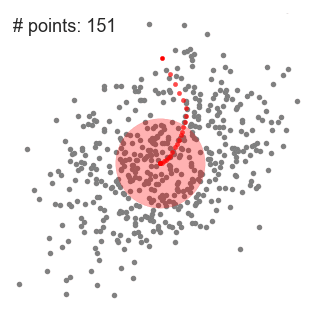
An illustration of the entire process from end-to-end with all of the sliding windows is show below. Each black dot represents the centroid of a sliding window and each gray dot is a data point.

In contrast to K-means clustering there is no need to select the number of clusters as mean-shift automatically discovers this. That’s a massive advantage. The fact that the cluster centers converge towards the points of maximum density is also quite desirable as it is quite intuitive to understand and fits well in a naturally data-driven sense. The drawback is that the selection of the window size/radius “r” can be non-trivial.